CS325 Compiler Design
Lecture 1 – October 4th, 2017
Missed…
Lecture 2 – October 6th, 2017
Part 1 Lexical Analyzer (Lexing)
Lecture 3 – October 9th, 2017
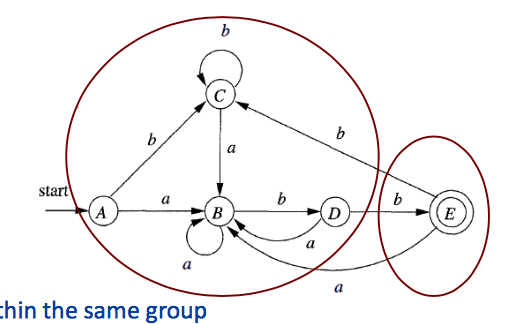
DFA to minimal DFA: Hopcroft’s algorithm
- Given states in the DFA partition the states into two groups – and , the accepting states and the nonaccepting states. Denote this initial partitioning as , .
- Let new partitioning
For each group in
partition into subgroups such that two states and are in the same subgroup if and only if for all input symbols
Part 2 Syntax Analyzer (Parsing)
Overview
-
Context free grammars (CFGs) – formal mechanism for
- specifying the syntax of the source language and
- a systematic method of determining membership in this formally specified language
- we use context-free grammars to specify the grammatical structure of programming languages.
-
Algorithms for doing this:
- Top-down parsing – and recursive descent parsers.
- Bottom-up parsing – parsers, canonical parsers, LALR parser.
Regular expressions are not sufficiently powerful to represent context-free structures. It doesn’t understand recursion, for example.
Context Free Grammars (CFGs)
Formally
- – A set of terminal symbols
- – A set of nonterminals
- – A designation of one of the nonterminals as the start symbol
- – A set of productions, where each production consists of a nonterminal, called the head or left side of the production, an arrow and a sequence of terminals and/or nonterminal, called the body or right side of the production.
Backus-Naur form (BNF)
<SheepNoise> ::= baa <SheepNoise>
| baa- Nonterminal symbols wrapped in angle brackets
<SheepNoise> - Terminal symbols underlined.
- The symbol
::=means “derives,” and the symbol|means “also derives“
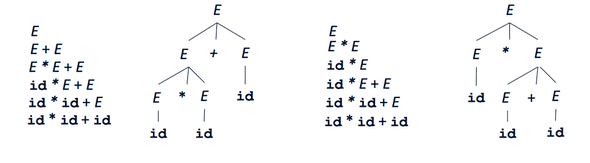
Ambiguous Grammars
Consider the grammar:
Now consider the input: id * id + id
This input can be derived in two different ways: